안녕하세요!
오늘은 머신러닝의 키워드 중 하나인 선형회귀의 장단점과 가중치(w)와 편향(b), 회귀 평가지표에 대해 소개해 드려요!
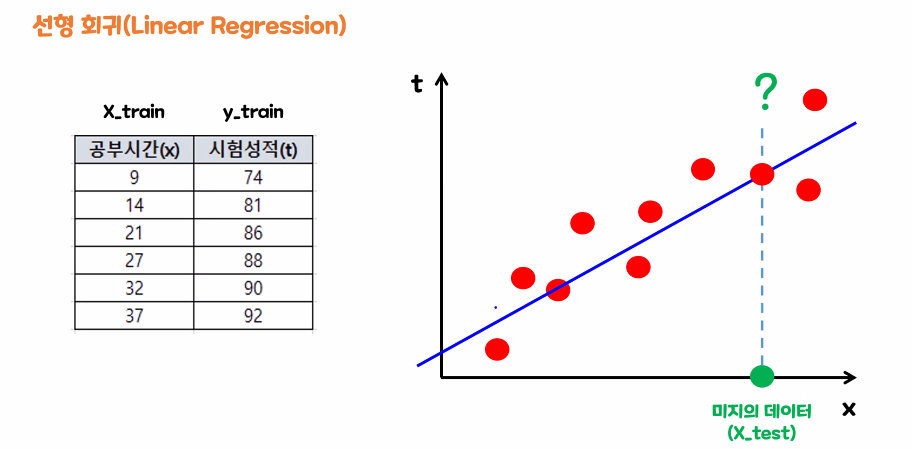
📍 선형회귀

- 선형 회귀는 직선의 형태를 가진 1차 식을 이용하여 연속된 수치값을 다루며 예측합니다.
- 컴퓨터가 데이터를 가장 잘 설명하는 하나의 직선을 바로 찾는 것이 아니라 여러 직선을 그어보면서 계산을 진행한 후 오차 값이 가장 작은 직선을 찾는 방법
📌 선형회귀를 구성하는 수식
y = wx + b
1차식, 단항 회귀식
회귀 분야는 실질적인 수치 값을 다루기 때문에 수식이 조금씩 들어갑니다.
- 가중치(w) – 각각의 특성들이 얼마나 예측에 영향을 미치는지(영향도) 결정하는 계수
- 편향(b) – 그래프를 수직 방향으로 이동시키는 계수
📌 회귀 평가지표
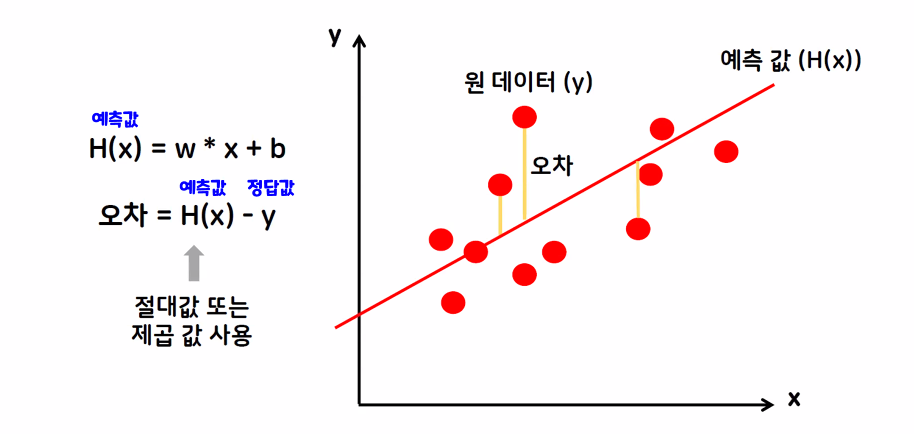
예측 값을 직선으로 그린 후 실제 데이터와의 오차가 얼마나 나는지 평가하는 지표
- MSE(평균제곱오차)
- 모든 오차를 제곱해서 평균을 구한다.
- RMSE(평균제곱근 오차)
- MSE 값이 제곱이 되어있어서 오차가 크기 때문에 제곱근을 씌워서 원래 크기로 돌려줌
- MAPE(평균 절대비율 오차)
- MSE, RMSE -> 예측 대상의 크기에 따라 성능 측정이 어렵다.(예시 : 실제 500 값의 오차 10과 실제 10000 값의 오차 10)
- 전체 크기에 백분율을 적용해서 같은 기준으로 만들어 준 다음 성능을 측정한다.
- R2 스코어(결정 계수)
- 회귀 함수가 실제 데이터의 평균에 비해 얼마나 데이터들을 잘 설명할 수 있는가?
- 일반적인 상황에서 0 ~ 1의 값을 가진다.
- 예측을 잘 못한 경우 -값이 나올 수도 있다.
📌 선형회귀의 장단점
Linear Model 장점
- 결과 예측 속도가 빠르다.
- 대용량 데이터에도 충분히 활용 가능하다.
- 특성이 많은 데이터 세트라면 훌륭한 성능을 낼 수 있다.
Linear Model 단점
- 특성이 적은 저차원 데이터에서는 다른 모델의 일반화 성능이 더 좋을 수 있다.
- 특성 확장을 하기도 한다.
- LinearRegression Model은 복잡도를 제어할 방법이 없어 과대 적합이 되기 쉽다.
- 모델 정규화(Regularization)을 통해 과대 적합을 제어한다.(L1, L2 정규화)
여기까지 선형회귀의 기본 개념이었습니다!