안녕하세요!
저번에는 선형회귀의 기본 개념에 대해 소개해 드렸었는데요.
이번에는 MSE가 최소가 되는 최적의 w, b 값을 구하는 방법에 대해 소개해 드려요.
📍 경사하강법

📌 정의
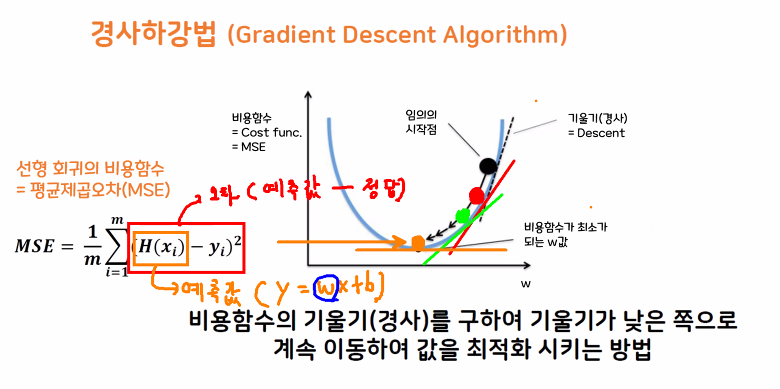
- 평균 제곱 오차(MSE)가 최소가 되게 하는 최적의 w, b 값을 찾는 방법론입니다.
- 기계가 스스로 학습한다는 머신, 딥러닝의 개념을 있게 한 핵심 알고리즘
- 기울기가 0이 될 때 최적의 가중치가 되고 최적의 w가 되는 것입니다.
- 여기서 최적의 가중치를 찾을 때 발생하는 비용 함수는 평균 제곱오차(MSE)입니다.
📌 가중치 값 갱신 과정
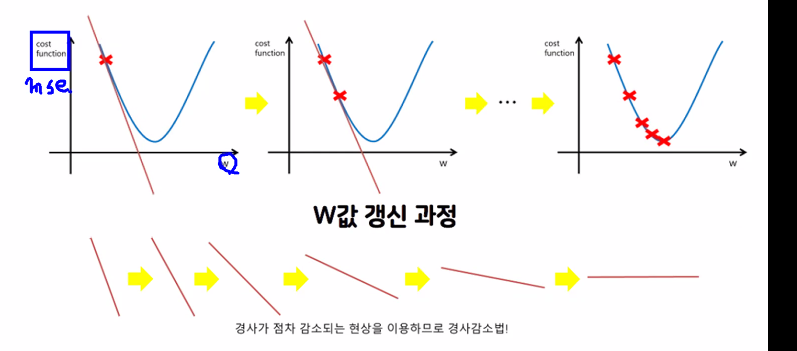
- 경사가 점차 감소되는 현상을 이용하는 방식입니다.
- 가중치 값을 점점 갱신하는 과정
📌 Learning rate
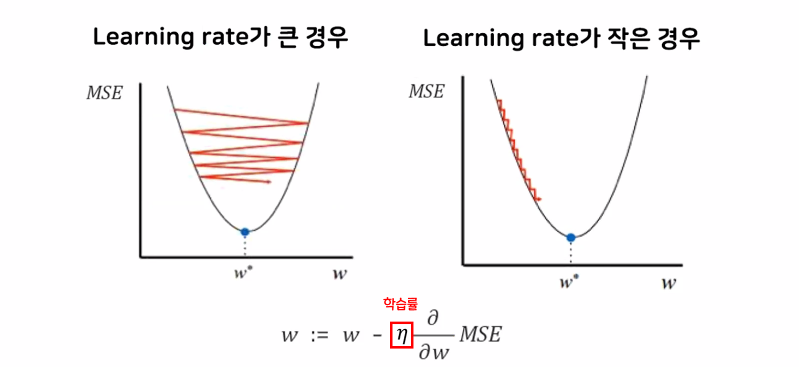
- Learning rate라는 학습률을 조정해서 최적의 가중치를 얼마 만에 도달할 것인지 조절한다.
- 학습률 = 보폭과 같은 개념
- Learning rate가 큰 경우 빠르게 최적의 값에 도달할 수 있지만 정확도가 좋지 않다.
- 작은 경우는 상대적으로 정확도가 좋지만 오래 걸리고 데이터가 많으면 불리하다.
📌 Learning rate 값에 대한 차이
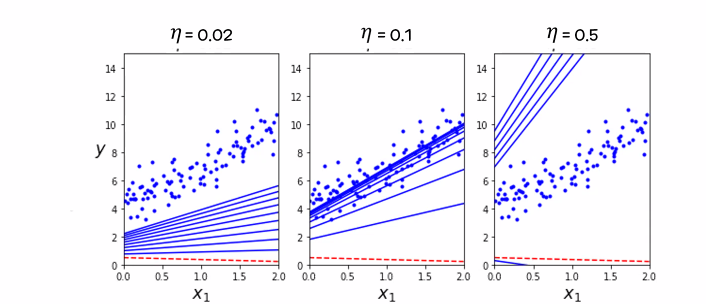
- 첫 번째 사진의 경우 학습률이 너무 작아서 최적의 값에 도달하지 못했다.
- 두 번째 사진의 경우 최적의 학습률을 이상적인 가중치 값을 찾았다.
- 세 번째 사진의 경우 학습률이 너무 높아 최적의 값을 넘어버렸다.
미분을 기반으로 하기 때문에 선의 최적값으로 가는 이동거리가 점점 줄어드는 특징을 가지고 있다.
📌 확률적 경사하강법
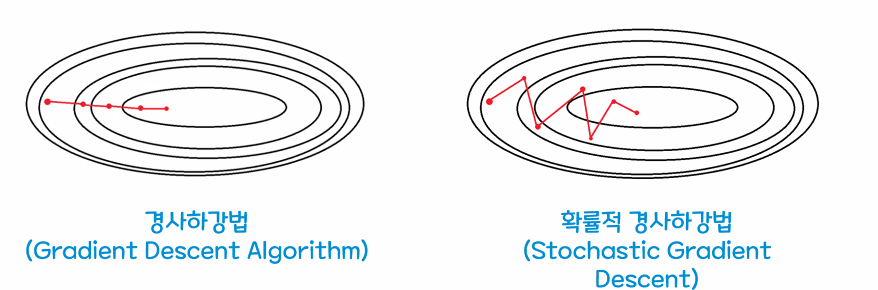
- 경사하강법(Gradient Descent Algorithm)
- 전체 데이터를 이용하여 경사를 구하기 때문에 최저점 수렴이 안정적이다
- 전체 데이터를 모두 한 번에 처리하기 때문에 속도가 느리고 메모리가 많이 필요함
- 확률적 경사하강법(Stochastic Gradient Descent)
- 전체 데이터 중 랜덤하게 선택된 하나의 데이터를 이용하여 진행한다.
- 적은 데이터로 학습할 수 있고 최적화 속도가 빠르다
- 하나의 데이터를 이용하기 때문에 기울기의 방향이 크게 바뀌고 오차율이 높아지므로 최저점 안착이 비교적 힘들다.
📌 미니 배치 확률적 경사하강법
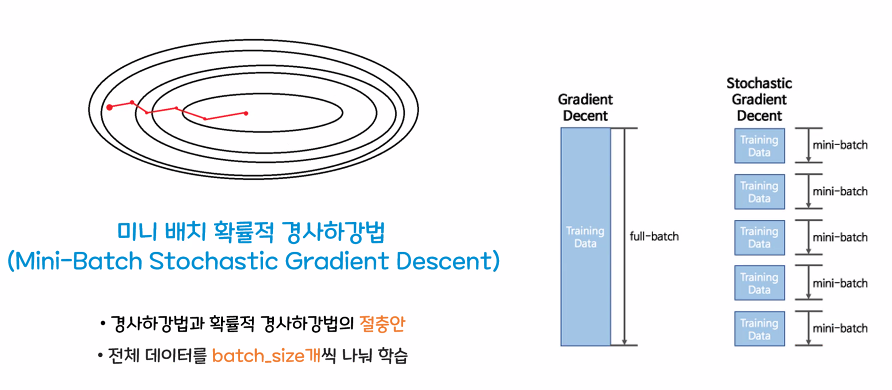
- 위의 두 방법을 절충하여 미니 배치 확률적 방법이 등장했다.
- 전체 데이터를 batch-size 개를 나눠 학습을 진행한다.
- 위의 두 방법의 장점이 존재한다.
여기까지 선형회귀에서 최적의 가중치를 찾는 경사하강법에 대해 알아보았습니다!
다음에도 다른 정보로 찾아오겠습니다!