안녕하세요!
오늘은 선형회귀의 단점, 과대 적합을 제어하는 머신러닝의 Regularization, L1(Lasso), L2(Ridge)에 대해 소개해 드려요.

📍 Regularization
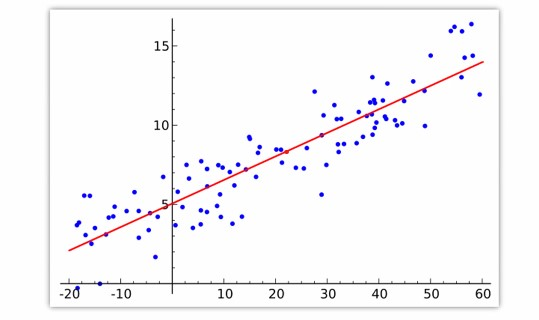
- 선형회귀 모델은 학습 데이터를 전부 반영하여 하나의 직선 방정식을 만들게 됩니다.
- 학습 데이터에 과대 적합이 되는 것을 방지할 수 있는 방법이 없다!
따라서 규제(정규화)를 사용하여 선형회귀 모델의 과대 적합 위험을 제어합니다.
- 가중치(w) 값의 비중을 줄이는 것!
📌 모델 정규화
y = w1x1 + w2x2+ w3x3+ w4x4 + … wpxp + b
다중 선형 회귀 함수식
다중 선형회귀 함수에서 w1, 과 w2의 값이 다르기 때문에 데이터가 들어오면 제대로 예측하지 못할 수 있어요.
예를 들어 w1가 1이고 w2이 10000이라면?
데이터가 들어왔을 때 w1 값이 무시가 되어 과대 적합이 걸릴 수 있다.
📌 L1(Lasso), L2(Ridge)
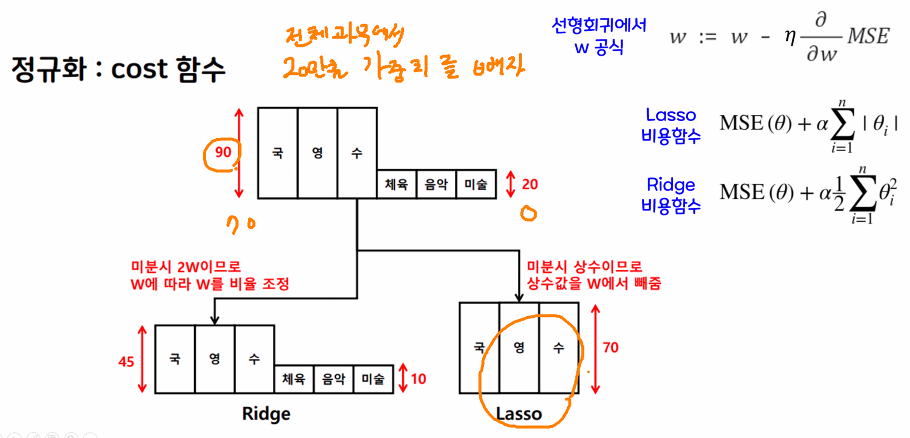
따라서 두 개의 정규화 방식으로 가중치의 값을 조절할 수 있어요.
Lasso
- 실제 값을 빼고 마이너스 가중치가 나오면 0으로 만듭니다.
- (예시) 가중치가 20, 30, 40이라면 임의로 25를 빼고 가중치를 0, 5, 15로 만드는 방법
- 0이 되면 특성을 제외합니다.
- 중요한 특성만 남길 때 아주 좋은 방법
Ridge
- 비율을 적용해서 큰 가중치를 조절합니다.
- (예시) 가중치가 20,30,40이라면 50%의 비율을 적용해서 10,15,20로 만드는 방법
- 가중치가 0이 나오지 않기 때문에 필요한 정보들을 모두 전달할 수 있습니다.
- 현업에서는 Ridge를 더 많이 사용하는 편
📌 Lasso 정규화 순서도

Lasso의 정규화 순서도는 다음과 같아요!
여기에서 alpha -> 규제 강도는 개발자인 저희가 조절합니다!
📌 L1, L2의 그래프 차이점
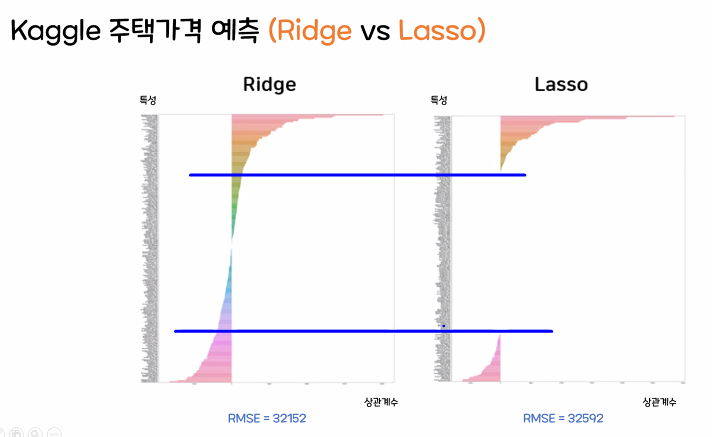
- Lasso 값은 특성 값이 사라져서 Ridge보다 값이 나오지 않는다.
- Ridge 값은 특성 값을 비율로 적용하기 때문에 값이 모두 살아있다.
여기까지 선형회귀의 단점, 과대 적합을 제어하는 머신러닝의 Regularization입니다